mpm580(我幫您)的部落格

三角函數的感覺

三角函數公式若需要用背的就是不理解

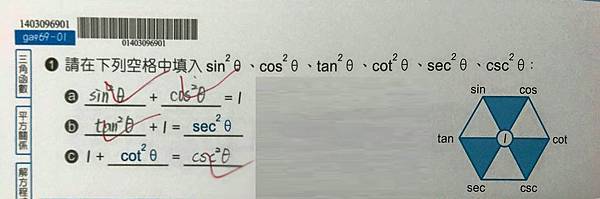
看似有規律，簡單好記

但你可知道為什麼嗎?

你對它有感覺嗎？

若是無感

只能靠記憶

需靠記憶則表示不解

過些時候可能就忘記了

數學家研究數學

從解決實務問題

可能經過無數的大師

不斷地演進

一直演變到最後抽象的描述

呈現在現代數學課本中

往往是非常簡潔的式子

看似簡易

若要由簡單的式子去了解

其實不是容易的事

學習新觀念如果不能理解

是很辛苦的

那麼就想辦法讓它有感覺

就理解了

三角函數的發展過程也不是一次就到位

發展過程中

有人用圓來觀察

角度大小和弦長的關係

弧長和弦長的關係

為了求得夾角變化時

所對應弦長 切線長 割線長 的變化

也有從斜率

來觀察對邊與鄰邊的變化

結合直角三角形的邊比關係

角(兩邊所夾)對應的弦線叫正弦(sin)

對應的切線叫正切(tan)

直角三角形的斜邊(即與圓的割線和切線相交的)為正割(sec)

 餘角(兩邊所夾)對應的弦線叫餘弦(cos)

 對應的切線叫餘切(cot)

直角三角形的斜邊(即與圓的割線和切線相交的)為餘割(csc) 

除了用漢字思考外

餘角和正角的關係

英文也是有含意的

字首co-是補、餘、互相之義

正弦  sine      餘弦  cosine

正切  tangent      餘切  cotangent

正割  secant      餘割  cosecant

 再依下圖來思考

這樣會比較容易理解

首先將圓的半徑設為1的單位圓

正角(藍色)對應正弦長、正切長及正割長(斜邊)

餘角(紅色)對應餘弦長、餘切長及餘割長(斜邊)

為了容易做比對

將餘角對應的餘弦、餘切移至藍色三角形的邊

利用上圖藍色(小中大)三個相似三角形的邊比關係

對邊 / 斜邊

sin θ / 1 = tan θ / sec θ = 1 / csc θ

對邊 / 鄰邊

sin θ / cos θ = tan θ / 1 = 1 / cot θ

鄰邊 / 斜邊

cos θ / 1 = 1 / sec θ = cot θ / csc θ

利用直角三角形的勾股定理

sin² θ + cos² θ = 1²

tan² θ + 1² = sec² θ

 1²  + cot² θ = csc² θ 

 這樣的觀察是有感覺的

不容易忘記

再由這些去演化出

一系列的關係(三角函數公式表)

看似簡潔易記 實不易理解

如

倒數關係

sin θ = 1 / csc θ

tan θ = 1 / cot θ

cos θ = 1 / sec θ

商數關係

sin θ / cos θ = tan θ =  sec θ / csc θ

cos θ / sin θ = cot θ =  csc θ / sec θ

平方關係

sin² θ + cos² θ = 1

 tan² θ + 1 = sec² θ  或  ( sec² θ - tan² θ = 1 )

  1 + cot² θ = csc² θ  或  ( csc² θ - cot² θ = 1 )

、

、

、

上述公式看起來很簡潔統一

但不易從公式去感覺它們的關係

就會想不通

愈簡潔的公式

愈不容易感覺

因為少了過程的陳述

但若先去了解它們的發展過程

澈底了解後

就會清楚明白了